Fun With Data: Fibonacci Trees

Glen Brunke, November 6, 2023

The Fibonacci Sequence Defined

Named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, this sequence of numbers has found its way into various realms of science, art, and even nature itself. The sequence is a series of numbers that begins with 0 and 1, with each subsequent number being the sum of the two preceding ones. Adding 0 to 1 gets you another 1, not too exciting so far, but now we add 1 to 1 and get 2. Next, we add 1 to 2 and get 3, then 2 and 3 gets us 5, and so on until we get a sequence that loosk like this...0, 1, 1, 2, 3, 5, 8, 13, 21, 34 and so on.

Who Was The Man Behind The Numbers?

Leonardo of Pisa, better known as Fibonacci, was an Italian mathematician who left an indelible mark on the world of mathematics. Born around 1170 in Pisa, Italy, he was one of the most influential mathematicians of the Middle Ages, and his contributions continue to shape the field of mathematics to this day.

Fibonacci's work was not fully appreciated during his lifetime, but it gained recognition in subsequent centuries. His contributions to mathematics were instrumental in the development of the modern numerical system and served as a bridge between the mathematical traditions of Europe and the Arab world. His "Liber Abaci" was instrumental in the spread of the Hindu-Arabic numeral system throughout Europe, ultimately leading to the abandonment of Roman numerals.

The Golden Ratio

One of the most intriguing aspects of the Fibonacci sequence is its connection to the golden ratio. The golden ratio, often denoted by the Greek letter φ (phi), is approximately equal to 1.618 and has been a subject of fascination for mathematicians, artists, and architects throughout history.

The relationship between the Fibonacci numbers and the golden ratio is evident when you take the ratio of two consecutive Fibonacci numbers as they grow larger. As you do so, the resulting ratio approaches the golden ratio.

Fibonacci in Nature

The Fibonacci sequence can also be observed in the natural world. In the growth patterns of many plants and flowers, the number of petals or seeds often follows a Fibonacci number. Sunflowers, for instance, typically have spirals of seeds that follow Fibonacci numbers. This pattern allows for efficient packing of seeds within the flower head.

Furthermore, the branching of trees, such as the way tree branches divide and subdivide, often adheres to the Fibonacci sequence. Nature seems to have a mathematical order that can be described by these simple numbers.

Putting Fibonacci To The Test

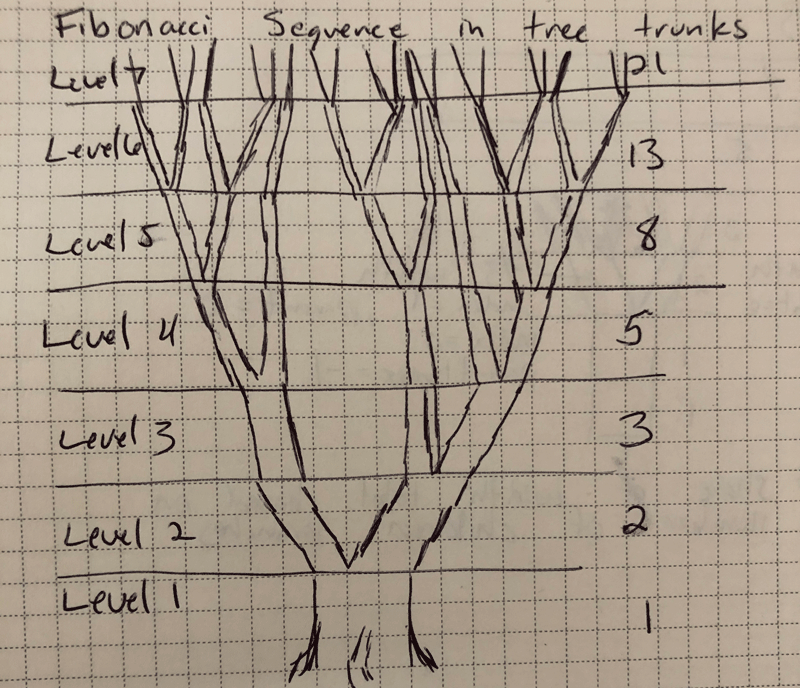
To put Fibonacci to a real-world test, I set out to build a tree generator that will draw trees according to the Fibonacci sequence. The width of each branch as well as the number of branches can both be determined with these rules. The result is a pretty passable tree in my opinion, take a look for yourself...



If you're interested in the source code, you can find it on my github repository.

How The Tree Is Built

The algorithm that produces the tree uses some simple rules and math to build the tree. First, we decide how many levels we want the tree to have (this is a random number between 3 and 9 in the above example). Each level has a number of branches based on the Fibonacci sequence. So we start with 1, branch into 2, then into 3, 5, 8 and so on. The size of the trunk (width) is determined by how many top level branches are on the tree. The program allocates the width to the branches depending on how many top level branches they are supporting, so smaller branches have less to support and vice versa.

We introduce some randomness into the tree so we have some natural-looking variety in lieu of industrial precision. Randomness can be found in the angles between branches and the splitting of branches, but each level remains proportional to maintain the sequence and visual balance.